Author: Joseph Iafrate
Editors: Christina Vallianatos, Scott Barolo, and Belle Moyers
*Editor’s Note: This post has several sound files to help readers understand the author’s message better. These sound files can be accessed via bolded links.
Part one of this post explained how physics gave us a new language for talking about musical notes. In part two, we look at combinations of notes. Will two notes sound pleasant together, or will they clash? We can apply what we’ve learned about frequencies to get an answer.
The Harmony of Ratios
If you’ve ever used the Pythagorean theorem, you are well-acquainted with one of Pythagoras’ contributions to society. Pythagoras was an ancient Greek philosopher and mathematician dedicated to discovering mathematical principles in the world around him. During his time, the Greeks already had an idea of which notes sounded good together, a pleasant combination of two or more notes that we call a harmony. Pythagoras and his followers could identify harmony by ear, but they wanted to see if the math that permeated the rest of their worldview had anything to say about this phenomenon.
According to legend, they took two taut strings of different lengths and plucked them at the same time. The sounds seemed to clash with one another. So the Pythagoreans increased the length of one of the strings and tried again. It was a bit better, but the notes still seemed to clash in their ears. So they increased the length again. This kept going until the sounds complemented one another. Eventually they got it just right, and the two notes were in harmony.
Pythagoras found a surprising result – the most pleasing harmonies happened when he could write the ratio of the string lengths as the ratio of two whole numbers, such as 4:3 or 3:1. The smaller these two numbers were, the more pleasant, or consonant, the harmony sounded. So, for example, 4:3 sounded better than 21:20.
Of course, the most obvious harmony is two identical strings, with a length ratio of 1:1. The next notable harmony occurred when one string was twice the length of the other, a ratio of 2:1. This is the simplest ratio of two different numbers, which today is known as the octave. Notice how the notes sound incredibly similar with one note “lower” and the other note “higher.” Those correspond to the longer and shorter string, respectively.
At the end of the day, we want to compare frequencies, for reasons we discussed last time. If the wavelengths have a ratio of 2:1, then the frequencies have the inverse ratio, 1:2. Doubling a frequency is called taking it “up an octave” and halving it is taking it “down an octave.” It follows then that four times the frequency is two octaves, eight times the frequency is three octaves, and so on. By convention, any power of two times a frequency is called the same note.
The next length ratio is 3:1. The notes are different, but they fit together well. One note sounds much “higher” than the other. The harmony will be more apparent to our ears if we double the length of the shorter string, lowering the note by an octave. We have a special name for this ratio: the fifth. This ratio is a staple of western music.
We can continue crafting ratios using increasing numbers. In Table 1, we build a standard major scale from a starting note (but be careful, we’re using frequency rather than length ratios). In this case, we will choose C as the starting note and compare other notes in the scale to the C. This simple scale goes from a note C to the C that is an octave higher and does not include sharps or flats. We’ll choose the starting note C4, often called “middle C.” The designation 4 tells us which octave the note lives in – notes with a larger number are higher and vice versa. Since C4 is defined as 261.626Hz (based on the assignment of A4 = 440Hz), C3 is 130.813Hz, C5 is 523.252Hz, and so on.* It is the ratios between the notes we generate that make this a major scale.
|
NOTE NAME |
FREQUENCY RATIO | ACTUAL FREQUENCY OF THE NOTE (Hz) | STRING LENGTH (MIDDLE C SHOWN IN ORANGE) |
| 1:1 | 261.626 |  |
|
| 9:8 |
294.329 |
 |
|
| 5:4 |
327.032 |
 |
|
| 4:3 |
348.835 |
 |
|
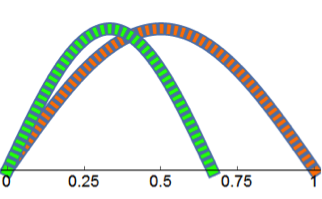
| 3:2 |
392.439 |
 |
|
| 5:3 |
436.043 |
 |
|
| 15:8 |
490.549 |
 |
|
| C | 2:1 |
523.252 |
 |
Table 1: We build up the major scale from C4. The first column gives the note names while the second column gives the ratio of the note frequency to the frequency of C4. This translates into the actual frequencies in column three. The final column shows the string lengths you would need to produce the desired notes, where the green string is the new note and the orange string is C4.
We have here established the major scale starting from C, but we have the tools to build around any starting note. Given a string of any length or a note of any frequency, we can use these same whole number ratios to construct a major scale for that new note, all thanks to physics!
Doing Physics by Ear
Being able to establish frequency ratios around an arbitrary frequency is a skill of great importance when playing in a band or orchestra. Musicians sometimes have to tune their instruments on the fly, whether or not a tuner is present. If you play a G to harmonize with your colleague’s C, it is far more important to maintain the correct 3:2 frequency ratio with their note than to match the tuner’s measurement of an exact G. In sharpening this skill, the musician is doing physics without even knowing it!
Just like that, a guitar string has shown us the physics underlying musical notes. We now have a numerical basis for talking about our notes, one that helps us to predict how well two of them will sound together. In future posts, we’ll look at alternate ways to build a scale and then investigate the relationship between time and frequency. All the while we’ll be able to lean on math to describe our favorite harmonies. Now that is music to a physicist’s ears!
*You may do a double-take when you see that A4 is not exactly 440Hz in Table 1, despite that being the frequency we started with to get C4. In fact, if you check our example frequencies against the official frequencies for these notes, you will see we are off by a few Hz in nearly every case. It turns out that trying to include more notes past a single major scale introduces new challenges that require a slightly different approach – a subject for another blog post.
About the author
Joe Iafrate just finished his third year in the Applied Physics PhD program at the University of Michigan. He studies the ways you can use light and electric fields to generate, control, and measure electron spins in semiconductors. Born and raised in Metro Detroit, Joe spent four awesome years in western Massachusetts at Williams College, graduating with a BA in Physics and Mathematics. Joe used to spend all his free time playing and arranging music for groups at Williams, but these days he spends most of his time following Major League Baseball and his favorite team, the Detroit Tigers. If you ever want to talk baseball or catch a game, feel free to reach out!
Read all posts by Joe here.
Image Credits:
Figures in Table 1: Joe Iafrate using Wolfram Mathematica 10.3 (Wolfram Research Inc., Champaign, IL, 2015)
misciwriters.com 